library(DescTools)
data <- read.table('https://raw.githubusercontent.com/shifteight/R-lang/master/TRB/data/yields.txt',
header=T, stringsAsFactors = TRUE)10 Anova
Si queremos predecir una variable Y de tipo continua, podemos dividir a grandes rasgos los tipos de modelos predictivos en tres grandes tipo en base a la naturaleza de los predictores o variables (X):

10.0.1 Tipos de modelos predictivos en R

10.1 ANOVA: Análisis de Varianza
Predecir Y usando una o más variables factoriales
Y ~ A; Y ~ A+B; Y ~ A+B+C
H0: μ1 = μ2 = μ3….(todas las medias poblacionales de Y son iguales, o no significativamente distintas)
H1: Al menos una media poblacional es distinta del resto
- No dice cual es la distinta!
Asume que:
- La selección de valores en los subgrupos es aleatoria e independiente
- Todas los subgrupos tienen una distribución de errores normal (residuos)
- Todas las poblaciones de los subgrupos de Y tienen la misma varianza
En caso que alguno de estos supuestos no se cumplan: Impactarán directamente sobre los valores p-valor reportados, y por lo tanto sobre la calidad de las conclusiones que finalmente buscamos obtener.
La verificación de los supuestos se realiza en la práctica a través de los predictores de los términos de error aleatorio que son los residuos aleatorios asociados a cada observación Por lo tanto los supuestos pueden verificarse mediante el análisis de los RESIDUOS.
10.2 On-Way ANOVA
ANOVA de unas sola cola, o comparación de una variable Y en un variable X de tipo factorial
Output del modelo simpre es:



10.3 Experimento factorial (Two-Way ANOVA)
En estas situaciones estimamos los parámetros para los efectos principales de cada nivel de dieta y cada nivel de suplemento, además de los términos para la interacción entre la dieta y el suplemento. Los grados de libertad de la interacción son el producto de los grados de libertad de los términos componentes (es decir, (3 - 1) × (4 - 1) = 6).
El modelo es gain~diet+supplement+diet:supplement, pero puede simplificarse utilizando la notación del asterisco así:
model <- aov(gain~diet*supplement)
summary(model)

Output del modelo Two-Way ANOVA :::
No hay evidencia de que las diferencias que dieta causa sobre Y (gain) varían en función de los suplementos, y viceversa. En este caso se puede decir entonces que los efectos de dieta y suplementos son Aditivos!
10.4 Pseudoreplicación: Diseños anidados y parcelas divididas
Los modelos ANOVA tienen la facilidad de tratar con estructuras de error complicadas, y es importante que puedan reconocer tales estructuras de error, y por lo tanto evitar posibles trampas de la pseudoreplicación.
Hay dos casos generales:
Muestreo anidado, como cuando se toman medidas repetidas del mismo individuo, o se realizan estudios observacionales donde datos se llevan a cabo en varias escalas espaciales diferentes (principalmente efectos aleatorios);
Análisis de parcelas divididas, como cuando los experimentos diseñados tienen diferentes tratamientos aplicados a parcelas de diferentes tamaños (en su mayoría, efectos fijos).
10.4.1 Parcelas divididas
Se aplican diferentes tratamientos a parcelas de diferentes tamaños. Cada tamaño de parcela tiene su propia varianza de error asociada, por lo que en lugar de tener una varianza de error (como en todas las tablas de ANOVA hasta este punto), tenemos tantos términos de error como tamaños de parcela diferentes. El análisis se presenta como una serie de tablas de ANOVA de componentes, una para cada tamaño de parcela, en una jerarquía que va desde el tamaño de parcela más grande con la menor replicación en la parte superior, hasta el tamaño de parcela más pequeño con la mayor replicación en la parte inferior.
Ejemplo: un experimento de campo diseñado sobre el rendimiento de los cultivos con tres tratamientos: riego (con dos niveles, regado o no), densidad de siembra (con tres niveles, bajo, medio y alto), y aplicación de fertilizantes (con tres niveles, bajo, medio y alto).
Las parcelas más grandes fueron los cuatro campos completos (bloque), cada uno de los cuales se dividió por la mitad, y el riego se asignó al azar a una mitad del campo. Cada parcela de riego se dividió en tres, y se asignó al azar una de las tres densidades de siembra diferentes (baja, media o alta) (independientemente para cada nivel de riego y cada bloque). Por último, cada parcela de densidad se dividió en tres, y se asignó al azar uno de los tres tratamientos de nutrientes fertilizantes (N, P, o N y P juntos).
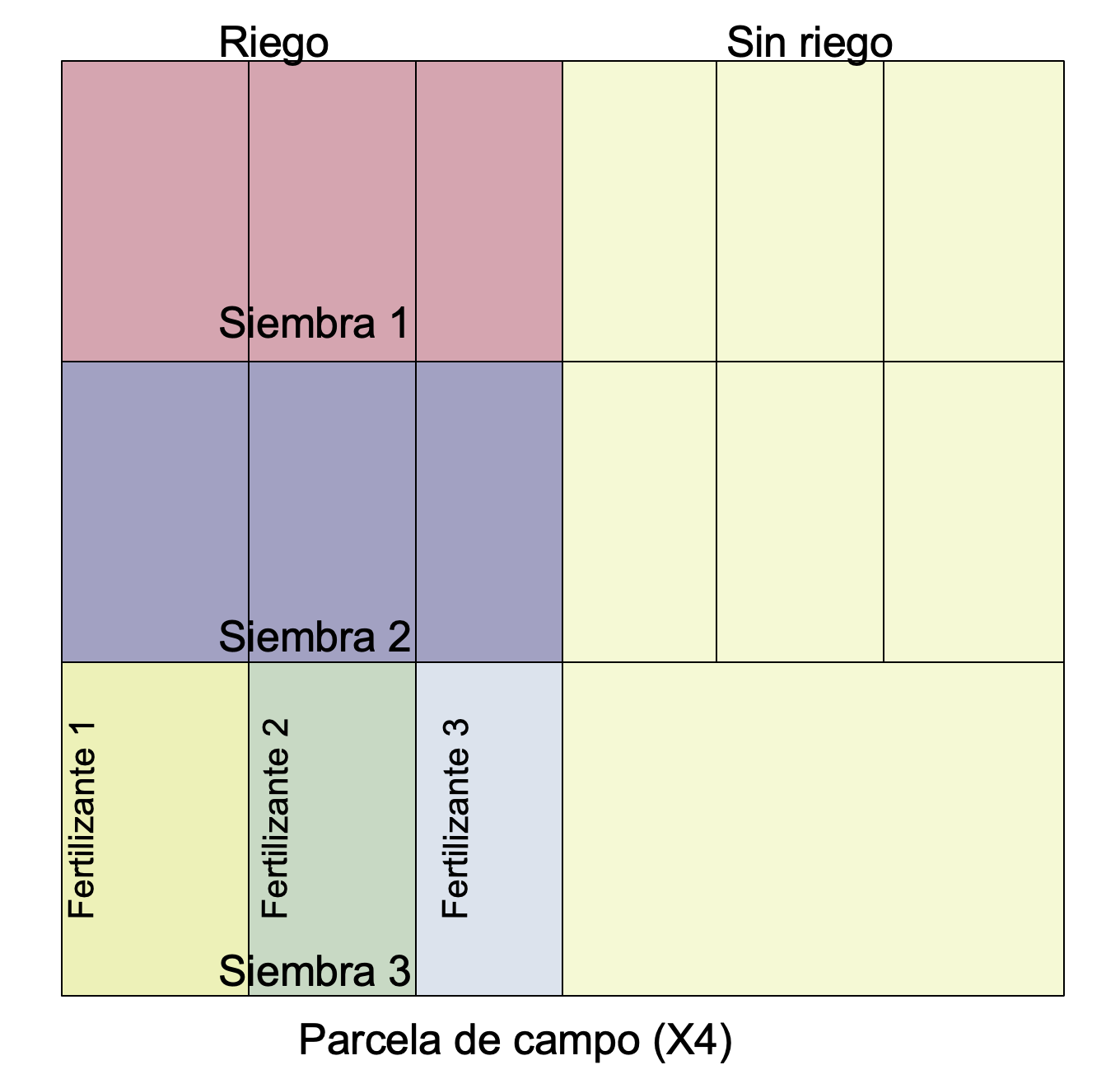
El problema de los experimentos con parcelas divididas es la pseudoreplicación.
En el ejemplo, hay cuatro bloques, cada uno dividido por la mitad, con una mitad regada y la otra como control. En caso específico del factor riego, el experimento debería contener sólo 8 filas (no 72 filas como en el presente caso). Debería tener d.f. = 7: tres para los bloques, uno para el riego y sólo 7 - 3 - 1 = 3 d.f. para el error.

Si no se ha detectado esto, el modelo podría ejecutarse con 51 f.d. que representan una pseudoreplicación masiva (el valor de p-valor correcto para el tratamiento de riego es 0,0247, pero en una ANOVA normal el error pseudoreplicado da p-valor = 2.81 × 10^{-10}).
Ej.,modelo factorial, usando todas las combinaciones entre factores (asteriscos en formula; *)
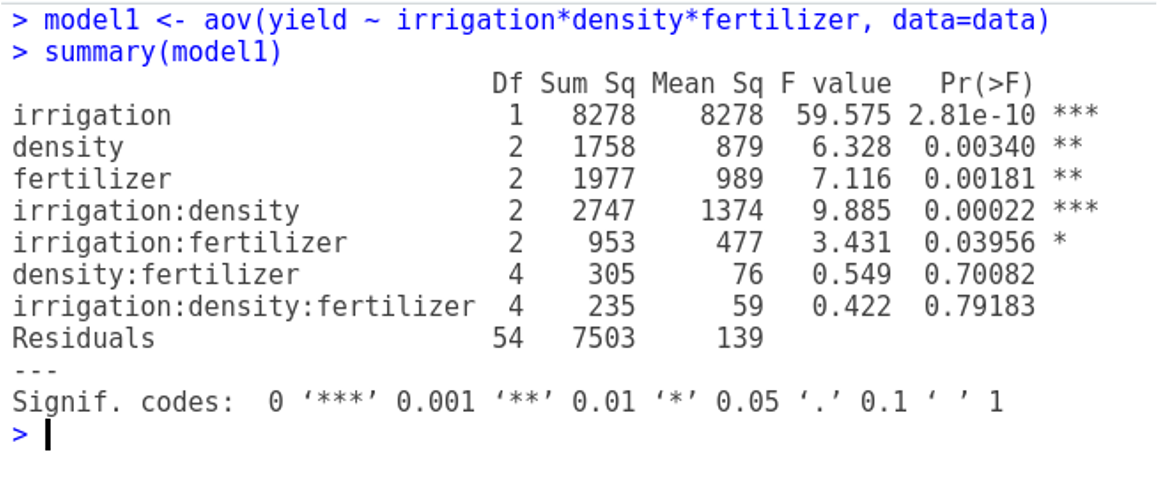
Para corregir esto, la estructura del error se define en el término Error, con los tamaños de parcela enumerados de izquierda a derecha, de mayor a menor, con cada variable separada por el operador de barra diagonal /. Tenga en cuenta que el tamaño de parcela más pequeño, el fertilizante, no necesita aparecer en el término Error:
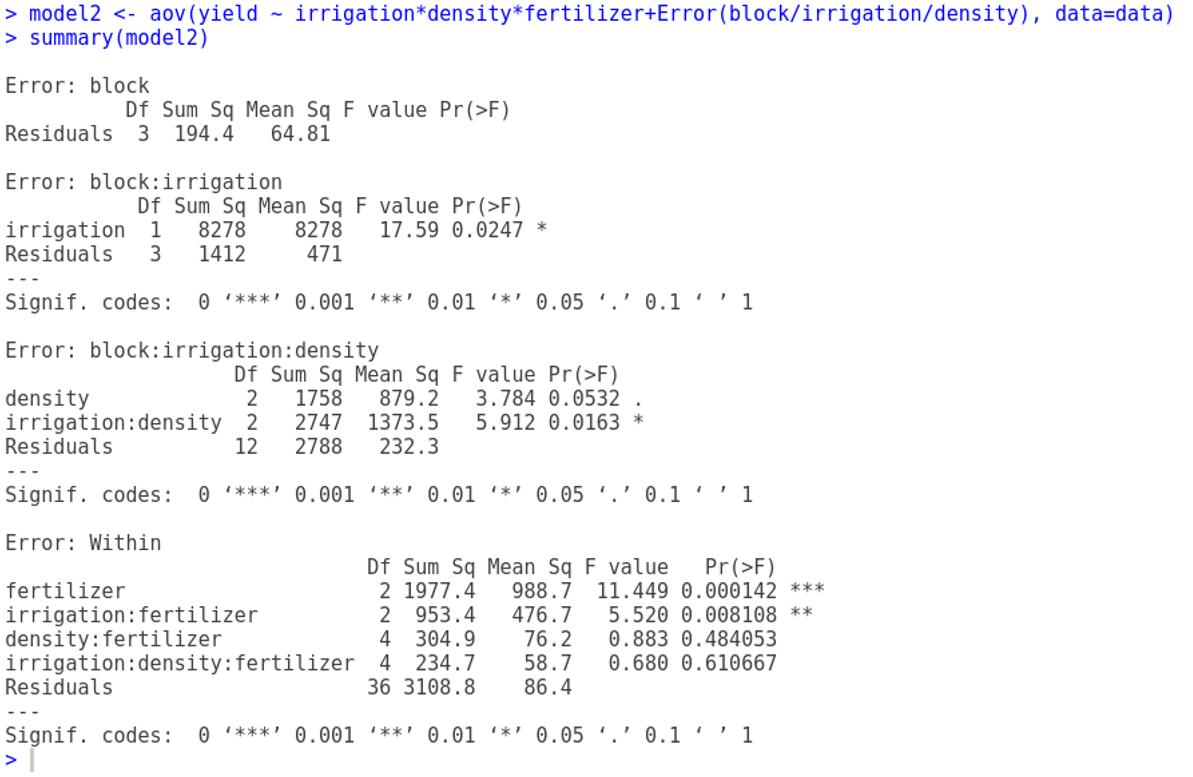
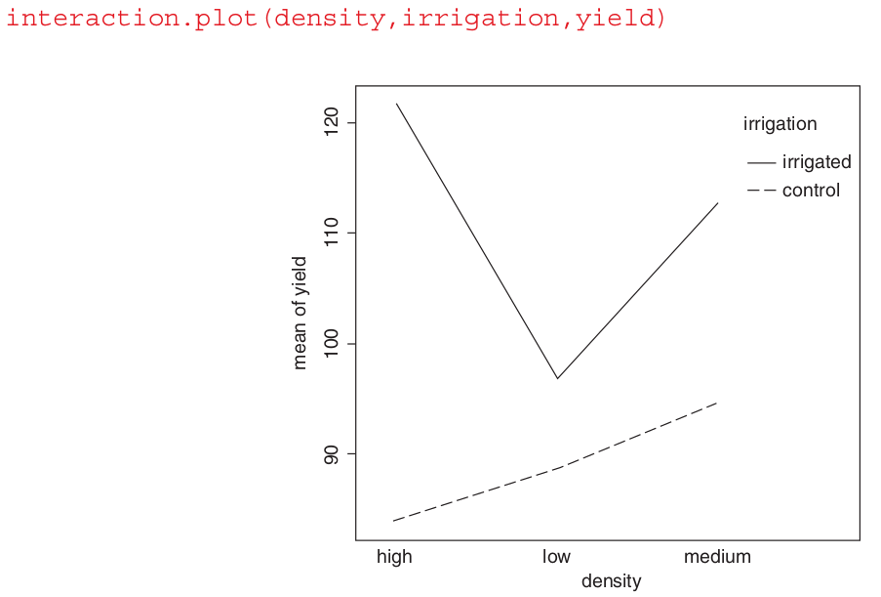
Nótese que el efecto principal no significativo de la densidad (p = 0,053) no significa que la densidad no sea importante, porque la densidad aparece en una interacción significativa con el riego (los términos de densidad se anulan, cuando se promedian en los dos tratamientos de riego; véase más adelante). La mejor manera de entender los dos términos de interacción significativos es trazarlos utilizando interaction.plot de la siguiente manera:
irrigation:fertilizer relationship
10.4.2 Muestreo Anidado
En este caso, hay un posible gradiente que se quiere ELIMINAR del análisis, para centrarse bien en el gradiente o efecto que SI es interesante. Ejemplo:
Se tiene una plantación de paltos en una ladera de cerro, y se quiere ver el efecto de fertilizantes y densidad de cultivo. Cómo la ladera de cerro puede tener mucho efecto en los resultados, debido a efectos de pendiente, características del suelo, etc., lo más importante acá es eliminar el efecto ladera-suelo del análisis.
Diseño de muestreo estratificado por ladera: clasificar 3 tipos de ladera (baja, media y alta) y hacer las MISMAS mediciones de fertilizante y densidad en las 3 clases de ladera. Finalmente, se agrega la info del bloque como factor para ser si efecto independiente.
aov(yield ~ fertilizer + density + block, data = block)

10.5 Sección Práctica Anova
10.5.1 Tratamiento a los Datos
# estructura de los datos
str(data)'data.frame': 10 obs. of 3 variables:
$ sand: int 6 10 8 6 14 17 9 11 7 11
$ clay: int 17 15 3 11 14 12 12 8 10 13
$ loam: int 13 16 9 12 15 16 17 13 18 14summary(data) sand clay loam
Min. : 6.00 Min. : 3.00 Min. : 9.0
1st Qu.: 7.25 1st Qu.:10.25 1st Qu.:13.0
Median : 9.50 Median :12.00 Median :14.5
Mean : 9.90 Mean :11.50 Mean :14.3
3rd Qu.:11.00 3rd Qu.:13.75 3rd Qu.:16.0
Max. :17.00 Max. :17.00 Max. :18.0 # se pueden juntar las 3 clases en una sola columna y agregar las clases en otra con la
# funcion stack
data2 <- stack(data)
colnames(data2) <- c("yield","soil") # cambiamos el nombre de las columnas
str(data2)'data.frame': 30 obs. of 2 variables:
$ yield: int 6 10 8 6 14 17 9 11 7 11 ...
$ soil : Factor w/ 3 levels "sand","clay",..: 1 1 1 1 1 1 1 1 1 1 ...- La clase soil es de tipo factorial esto es fundamental
10.5.2 Test de Bartlett
Analizar si las varianza por subgrupo es homogeneas con test de Bartlett, este test no necesita hacerse sobre los residuos
- H0 = son homogeneas
- H1 = no son homogeneas
### Test de Bartlett
bartlett.test(yield ~ soil, data = data2)
Bartlett test of homogeneity of variances
data: yield by soil
Bartlett's K-squared = 1.2764, df = 2, p-value = 0.528310.5.3 one-way ANOVA
Realizar test anova usando la funcion aov. Esta es la funcion estandar para este tipo de analisis
anov1 <- aov(yield ~ soil, data = data2)
summary(anov1) Df Sum Sq Mean Sq F value Pr(>F)
soil 2 99.2 49.60 4.245 0.025 *
Residuals 27 315.5 11.69
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1summary.lm(anov1)
Call:
aov(formula = yield ~ soil, data = data2)
Residuals:
Min 1Q Median 3Q Max
-8.5 -1.8 0.3 1.7 7.1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.900 1.081 9.158 9.04e-10 ***
soilclay 1.600 1.529 1.047 0.30456
soilloam 4.400 1.529 2.878 0.00773 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.418 on 27 degrees of freedom
Multiple R-squared: 0.2392, Adjusted R-squared: 0.1829
F-statistic: 4.245 on 2 and 27 DF, p-value: 0.0249510.5.4 Normalidad de los Residuos
par(mfrow = c(2, 2))
plot(anov1)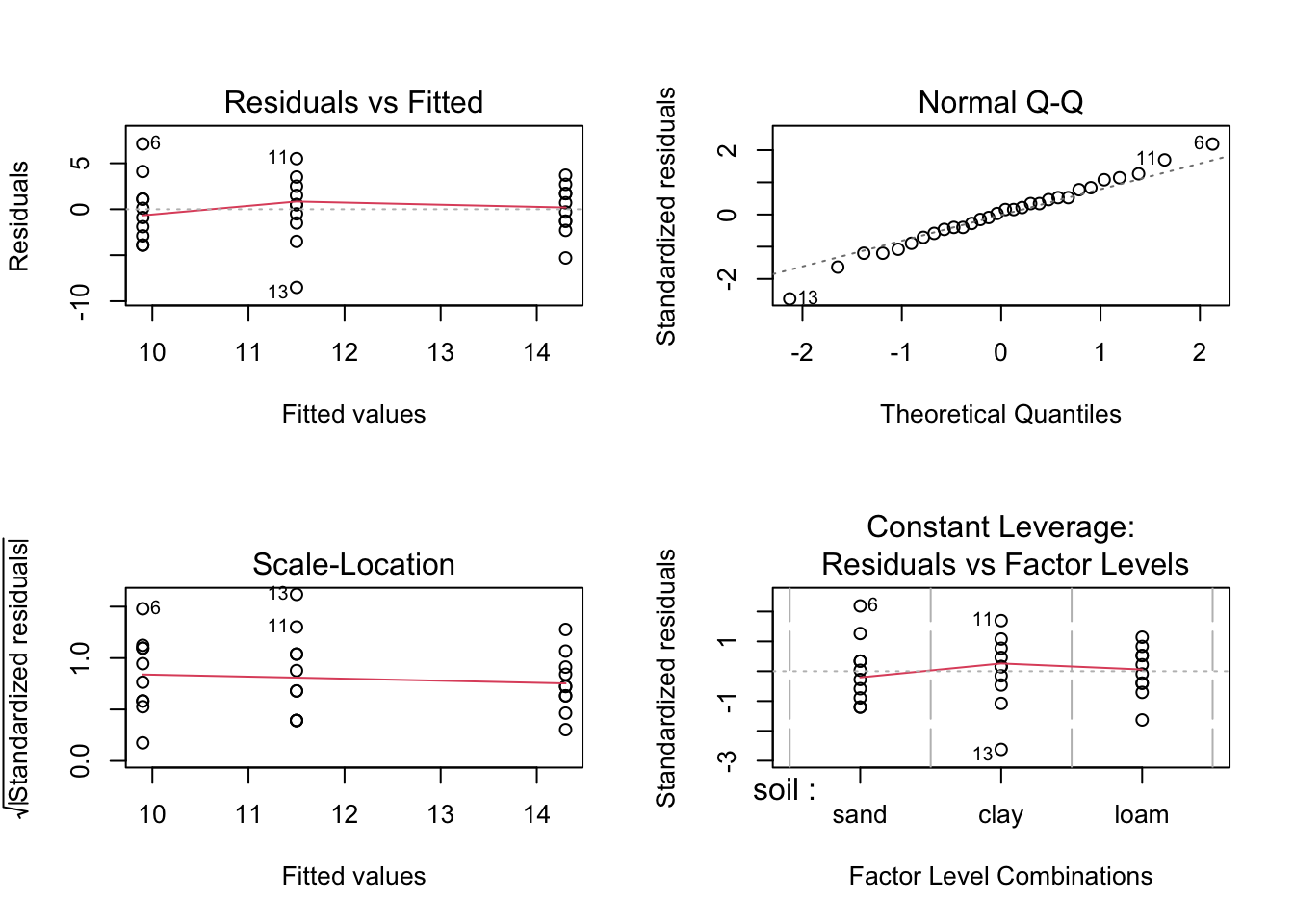
null device
1 - HO = es normal
- H1 = no es normal
shapiro.test(anov1$residuals) # si!
Shapiro-Wilk normality test
data: anov1$residuals
W = 0.99131, p-value = 0.996110.5.5 Post-Hoc
Necesitamos saber donde estan las diferencias entre clases
tuk <- TukeyHSD(anov1, conf.level = 0.95)
tuk Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = yield ~ soil, data = data2)
$soil
diff lwr upr p adj
clay-sand 1.6 -2.1903777 5.390378 0.5546301
loam-sand 4.4 0.6096223 8.190378 0.0204414
loam-clay 2.8 -0.9903777 6.590378 0.1785489plot(tuk, col = "red", las = 1, cex.axis = 0.5,
cex.lab = 0.5, cex = 0.5)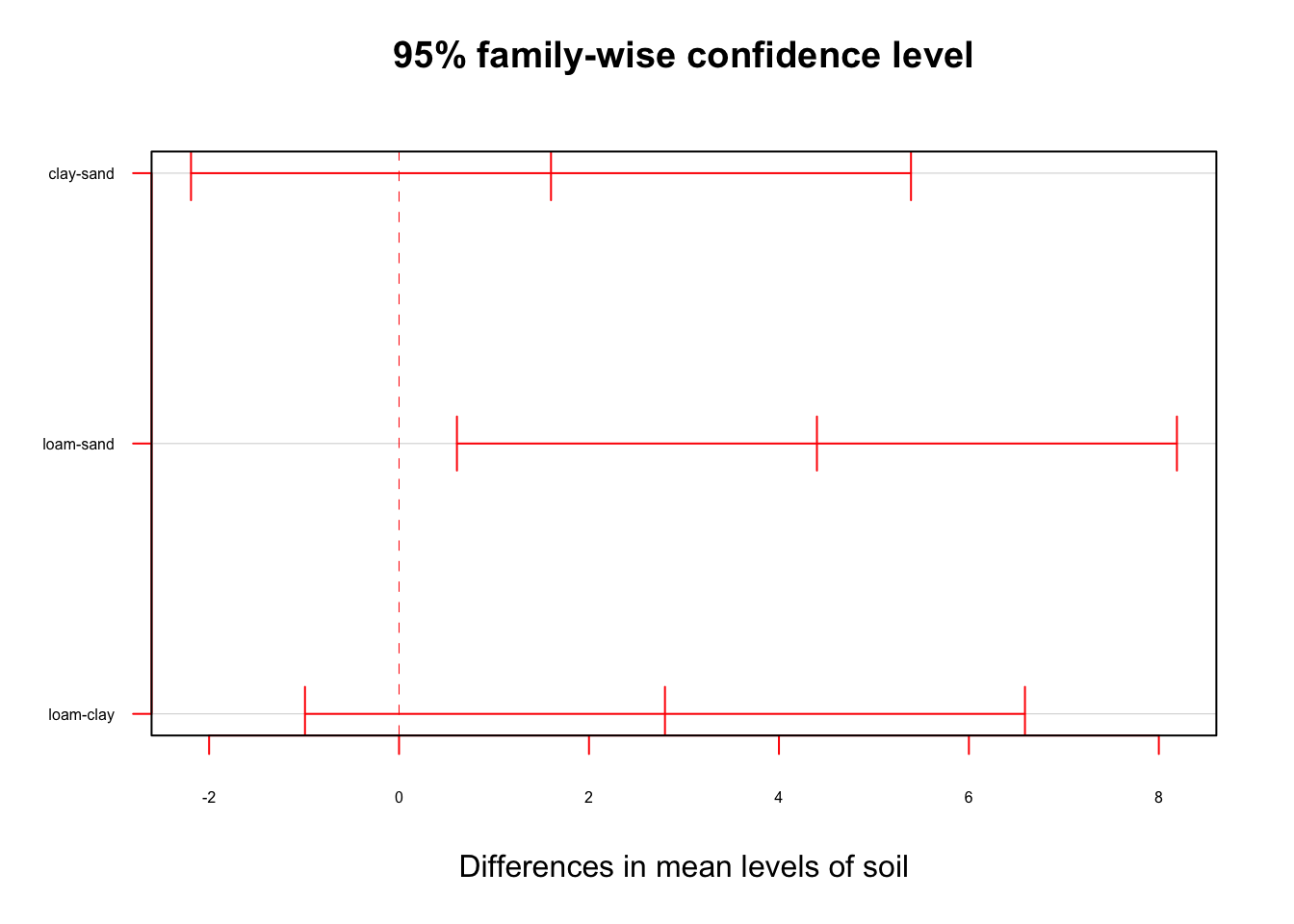
La diferencia entre loam y sand (limo y arena) es la unica significativa
10.5.6 Visualización
Boxplot*
boxplot(yield ~ soil, data = data2, col = 'lightblue', notch = T)Warning in (function (z, notch = FALSE, width = NULL, varwidth = FALSE, : some
notches went outside hinges ('box'): maybe set notch=FALSE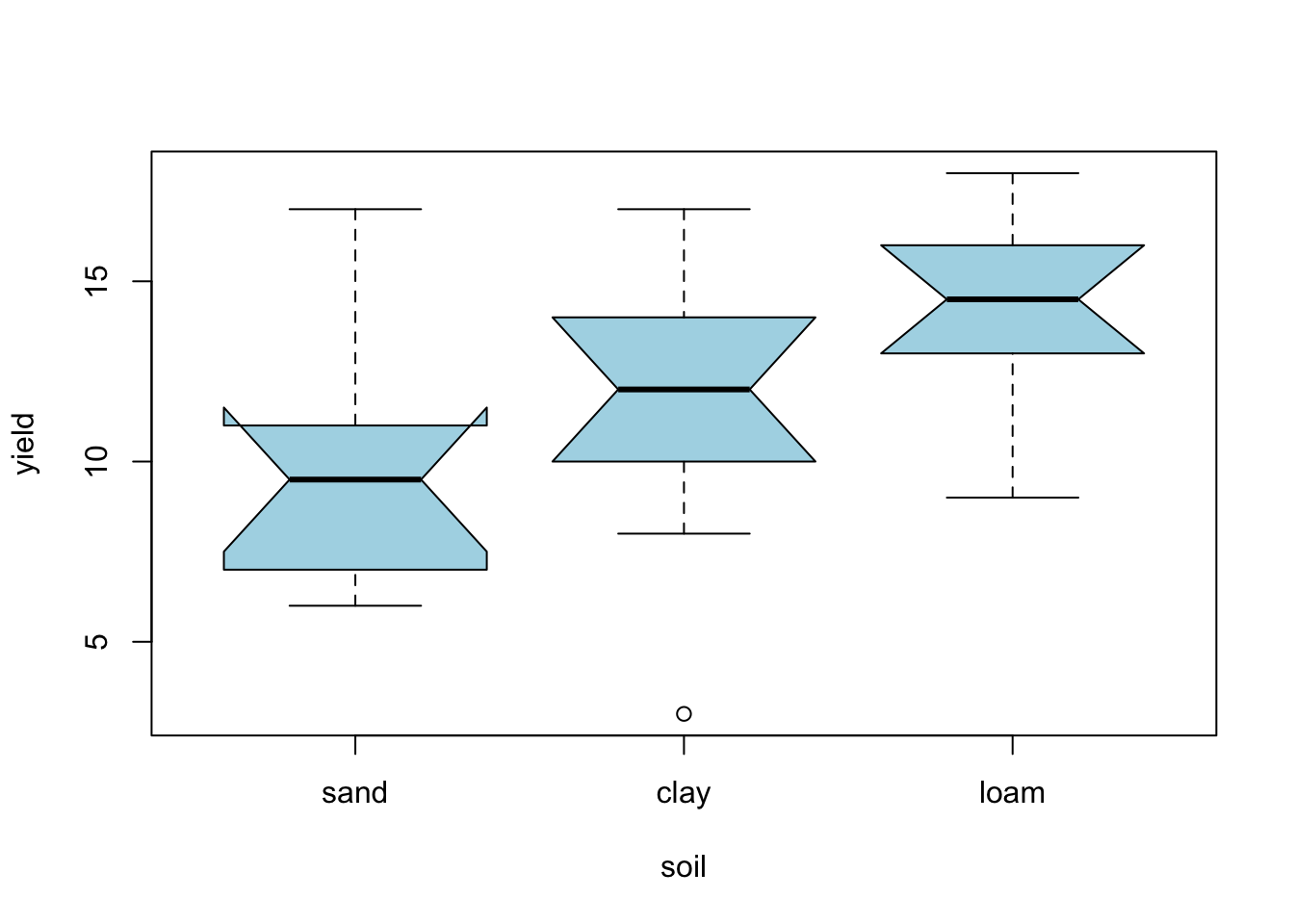
Barplot con barras de error
Revisar cuantas observaciones hay por clase. Ya sabemos que son 10, pero se puede revisar con table
table(data2$soil)
sand clay loam
10 10 10 Error estandar de una media = \sqrt(\frac{S2}{N}
summary(anov1) Df Sum Sq Mean Sq F value Pr(>F)
soil 2 99.2 49.60 4.245 0.025 *
Residuals 27 315.5 11.69
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# repetimos este valor por el numero de subclases
se <- rep( sqrt(11.69/10),3)
# Estimar las medias de los tres subgrupos
# La funcion tapply va a sacar la mean de yield usando como factor soil
ybar <- tapply(data2$yield, data2$soil, mean)
# Nombres de los subgrupos
labels <- levels(data2$soil)No hay una funcion para crear barras de error en R basico. Hay por su puesto en varios paquetes avanzados de plots, pero en este caso usamos esta funcion casera
error.bars <- function(yv,z,nn)
{xv <- barplot(yv,ylim=c(0,(max(yv)+max(z))),
col="gray",names=nn,ylab=deparse(substitute(yv)))
for (i in 1:length(xv)) {
arrows(xv[i],yv[i]+z[i],xv[i],yv[i]-z[i],angle=90,code=3,length=0.15)
}}error.bars(ybar, se, labels)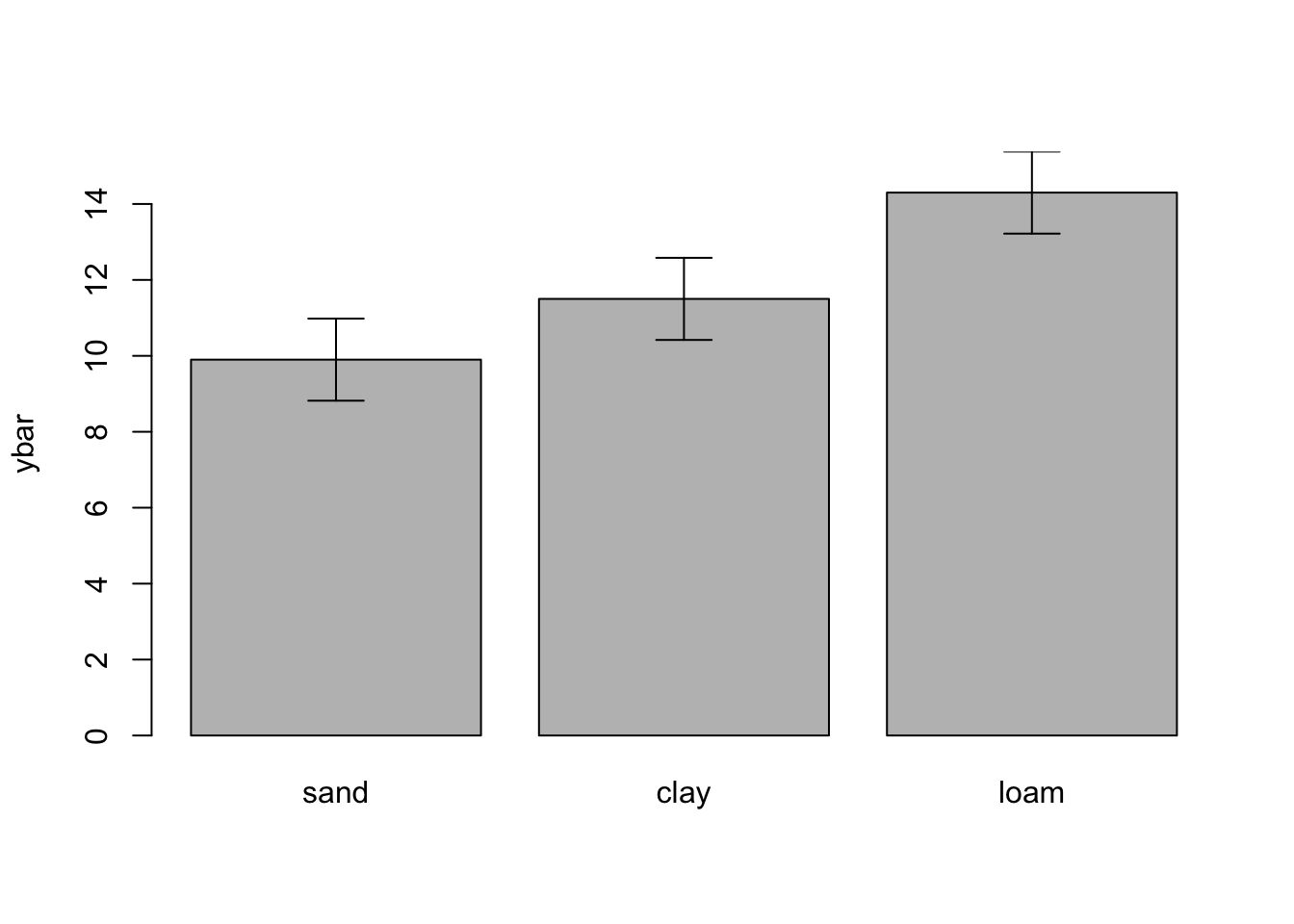
10.6 Ejemplo 2
one-way anova con tratamiento con control y post-hoc test de Dun
Ejemplo, examinar si dos nuevas tecnicas de ensenanza tienen potencialmente un beneficio en la nota final de un examen. Se dividen los estudiantes en 30 individuos en los siguientes grupos:
Control Group: 10 students New Study technique 1: 10 students New Study Technique 2: 10 students
data <- data.frame(technique = rep(c("control", "new1", "new2"), each = 10),
score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
77, 78, 79, 88, 89, 90, 91, 95, 95, 98))
head(data) technique score
1 control 76
2 control 77
3 control 77
4 control 81
5 control 82
6 control 82str(data)'data.frame': 30 obs. of 2 variables:
$ technique: chr "control" "control" "control" "control" ...
$ score : num 76 77 77 81 82 82 83 84 85 89 ...Asegurarse que de las clases o tratamientos esten en formato factorial!
data$technique <- as.factor(data$technique)
str(data)'data.frame': 30 obs. of 2 variables:
$ technique: Factor w/ 3 levels "control","new1",..: 1 1 1 1 1 1 1 1 1 1 ...
$ score : num 76 77 77 81 82 82 83 84 85 89 ...boxplot(score ~ technique,
data = data,
main = "Exam Scores by Studying Technique",
xlab = "Studying Technique",
ylab = "Exam Scores",
col = "steelblue",
border = "black")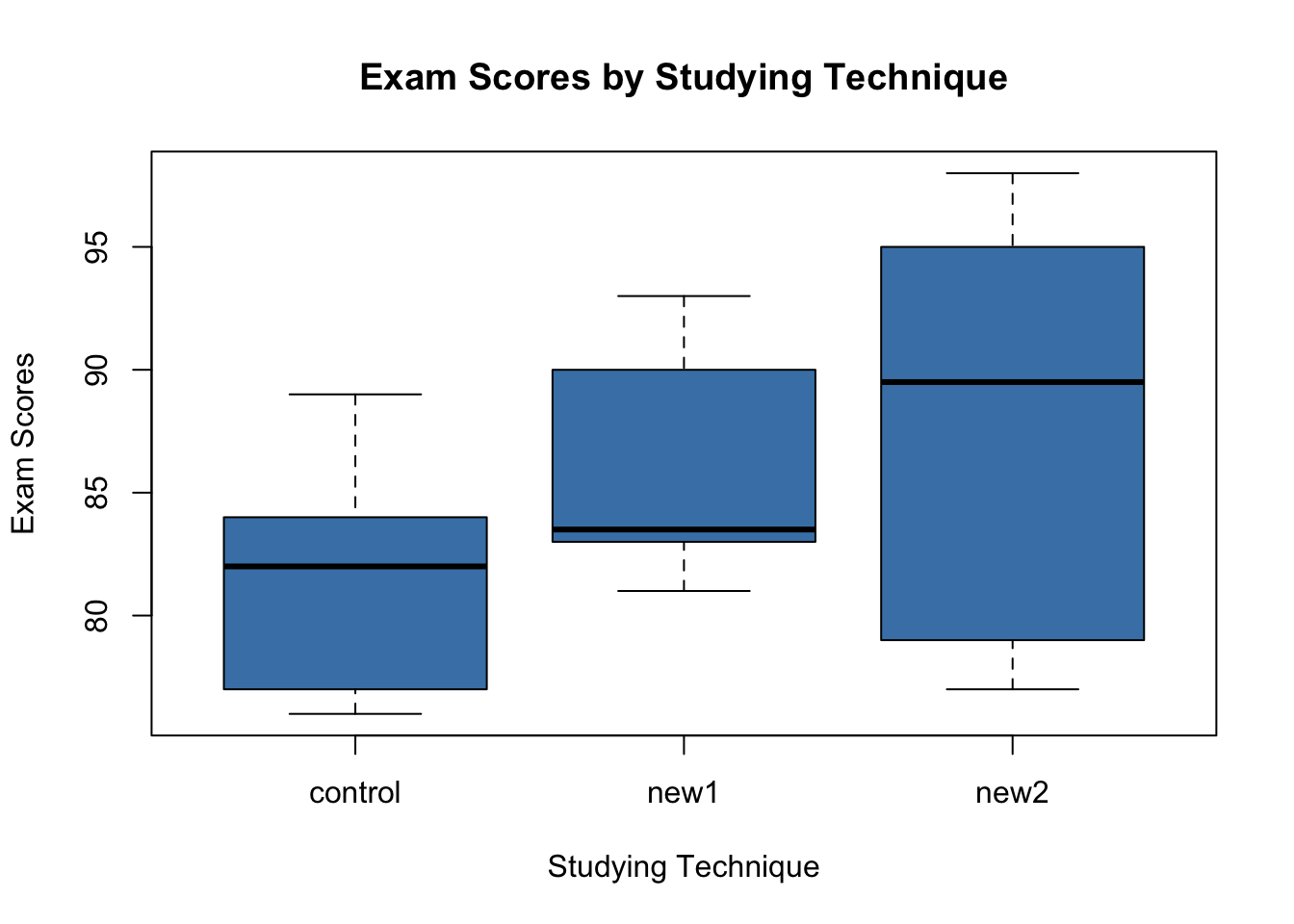
10.6.1 one-way ANOVA
model <- aov(score ~ technique, data = data)
summary(model) Df Sum Sq Mean Sq F value Pr(>F)
technique 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 110.6.2 Revision de residuos
par(mfrow = c(2, 2))
plot(model)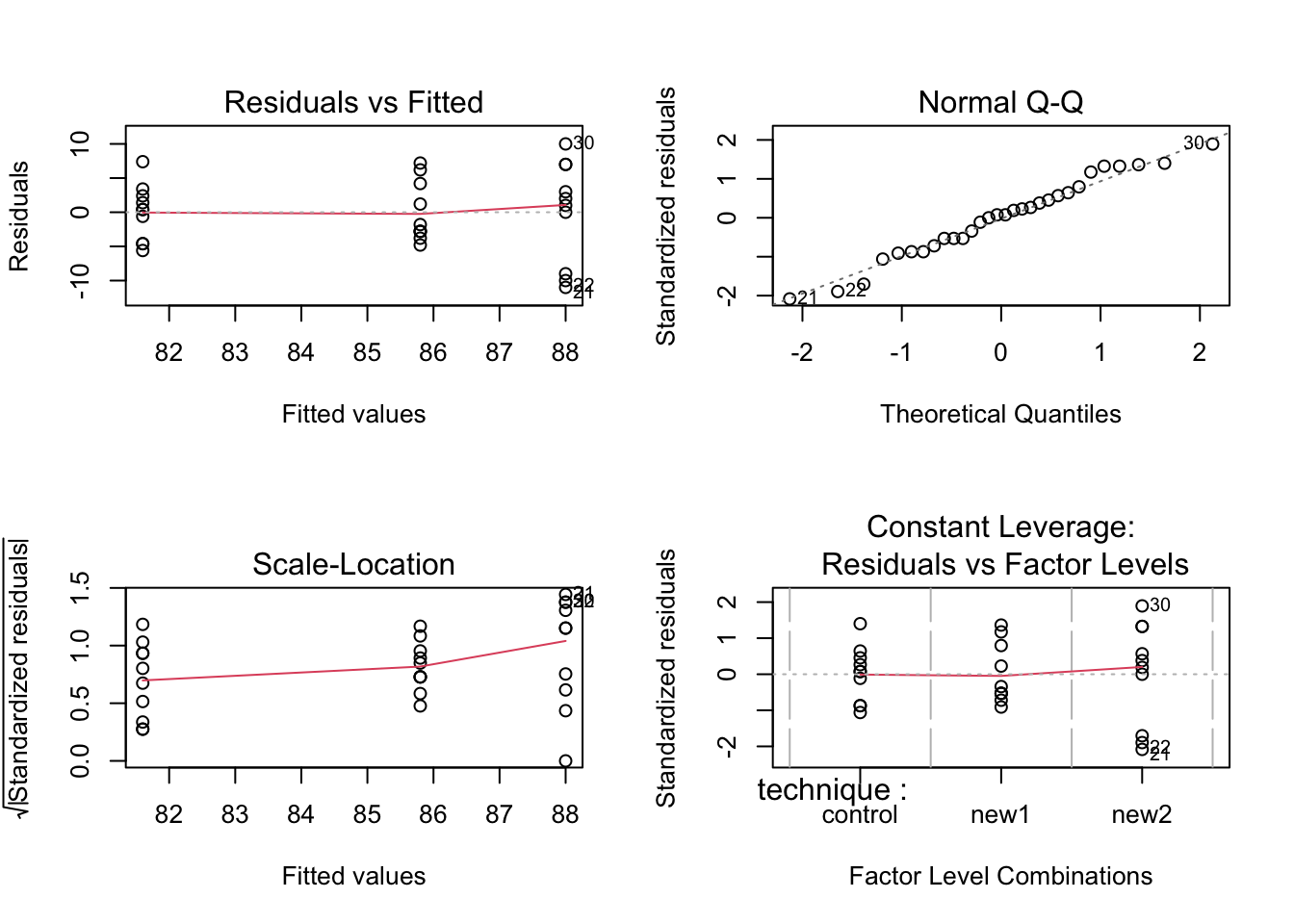
shapiro.test(model$residuals)
Shapiro-Wilk normality test
data: model$residuals
W = 0.97617, p-value = 0.7172null device
1 10.6.3 Test de Dunnett
compara solo las clases contra el tratamiento control
plot(DunnettTest(x = data$score, g = data$technique))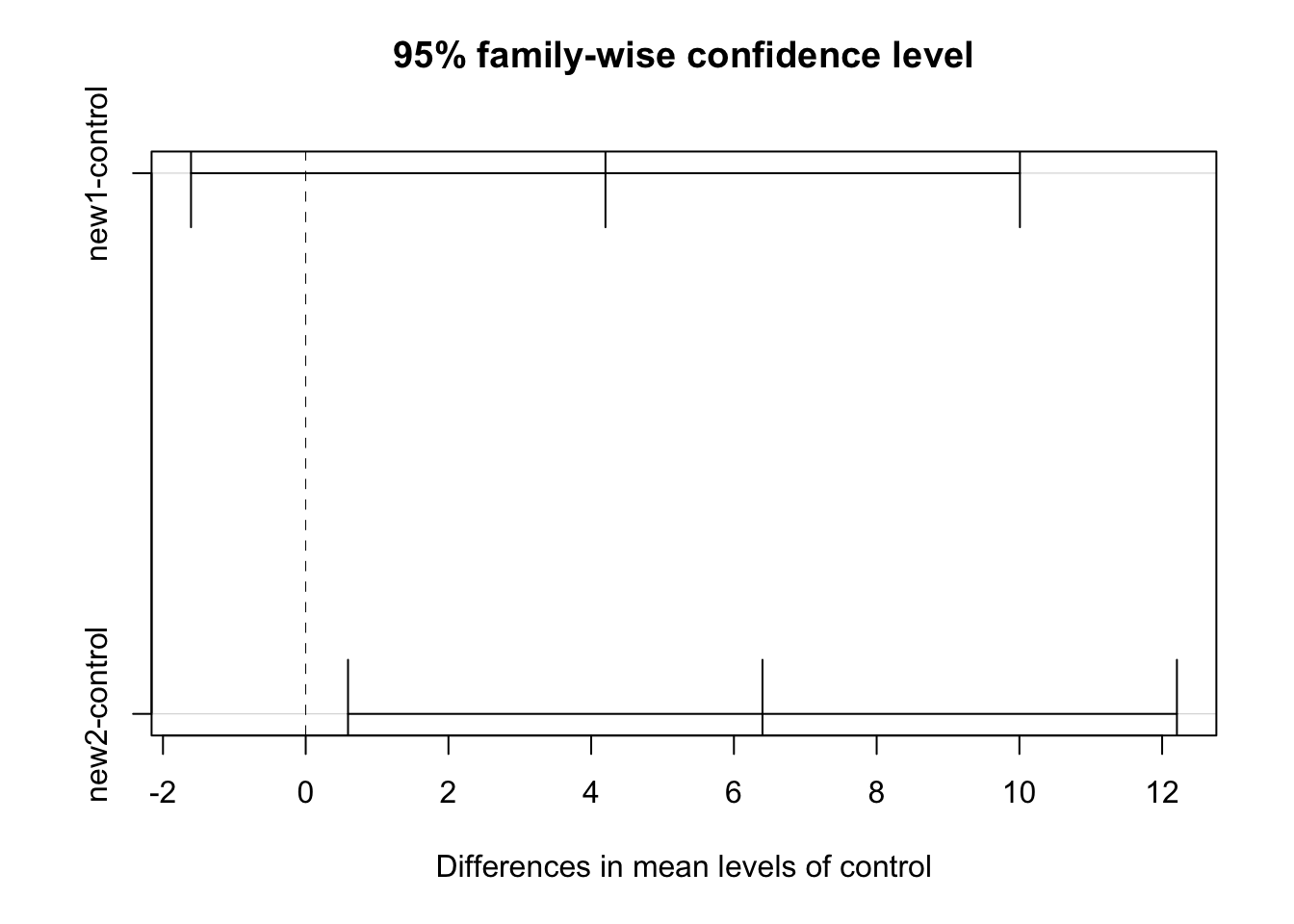
ASEGURARSE siempre que el control tenga el nombre ‘control’ exactamente en la tabla
10.6.4 PostHocs
la libreria DescTools tiene muchos test Post-hoc para hacer
10.6.4.1 Test de Tukey
Dos formas de visualizar el test de tukey
# Usando DescTools
PostHocTest(model, method = "hsd")
Posthoc multiple comparisons of means : Tukey HSD
95% family-wise confidence level
$technique
diff lwr.ci upr.ci pval
new1-control 4.2 -1.9700112 10.370011 0.2281
new2-control 6.4 0.2299888 12.570011 0.0409 *
new2-new1 2.2 -3.9700112 8.370011 0.6548
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# usando R
TukeyHSD(model) Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = score ~ technique, data = data)
$technique
diff lwr upr p adj
new1-control 4.2 -1.9700112 10.370011 0.2281369
new2-control 6.4 0.2299888 12.570011 0.0409017
new2-new1 2.2 -3.9700112 8.370011 0.6547756plot(PostHocTest(model, method = "hsd"))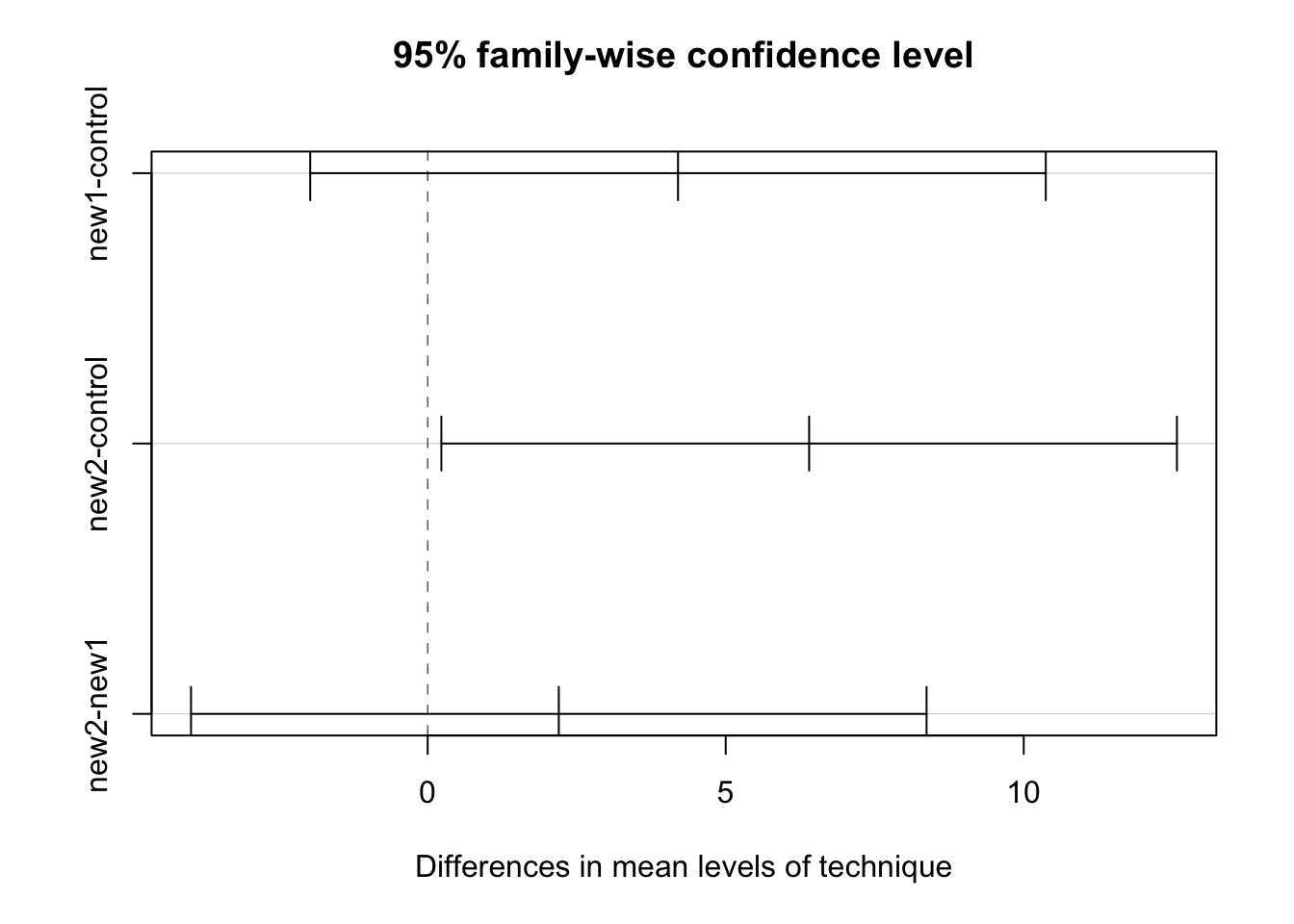
plot(TukeyHSD(model))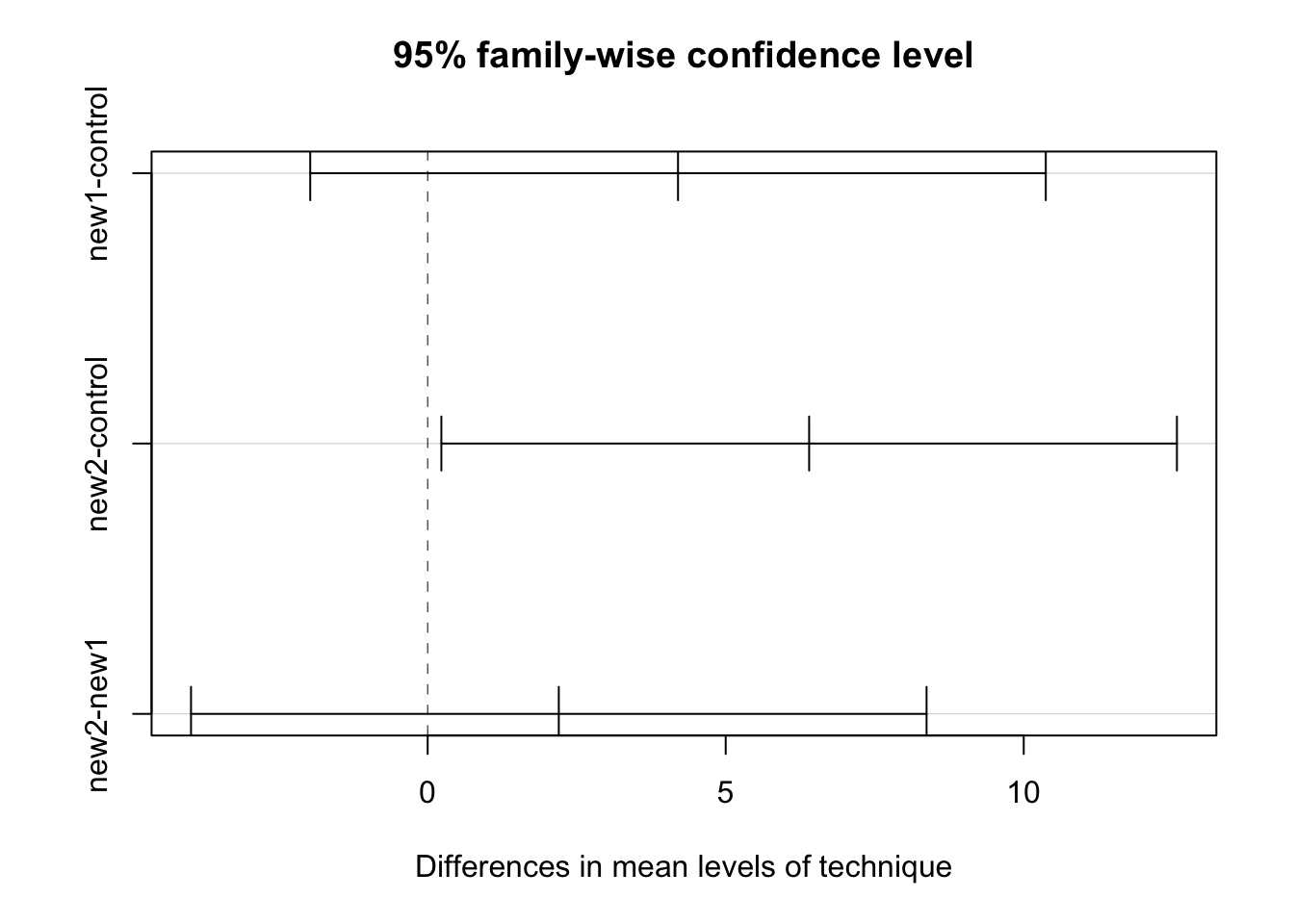
10.7 Experimento Factorial (two-way Anova)
10.7.1 Lectura Data
weights <- read.table('https://raw.githubusercontent.com/shifteight/R-lang/master/TRB/data/growth.txt',
header=T, stringsAsFactors = TRUE)
str(weights)'data.frame': 48 obs. of 3 variables:
$ supplement: Factor w/ 4 levels "agrimore","control",..: 3 3 3 3 2 2 2 2 4 4 ...
$ diet : Factor w/ 3 levels "barley","oats",..: 3 3 3 3 3 3 3 3 3 3 ...
$ gain : num 17.4 16.8 18.1 15.8 17.7 ...10.7.2 Barplot
inspeccion de datos con barplot. Primero, crear una tabla con promedios por clase usando tapply esta vez en tapply usamos una lista con los dos factores para que los tome a los dos en cuenta
ymean <- tapply(weights$gain, list(weights$diet, weights$supplement), mean)El parametro beside=TRUE indica que las subcalses (dieta) van como subgrupo del suplemento
barplot(ymean, beside = TRUE, ylim = c(0, 30), col = c("orange", "yellow", "cornsilk"))
labs <- c("Barley", "Oats", "Wheat")
legend('top', labs, fill= c("orange", "yellow", "cornsilk"))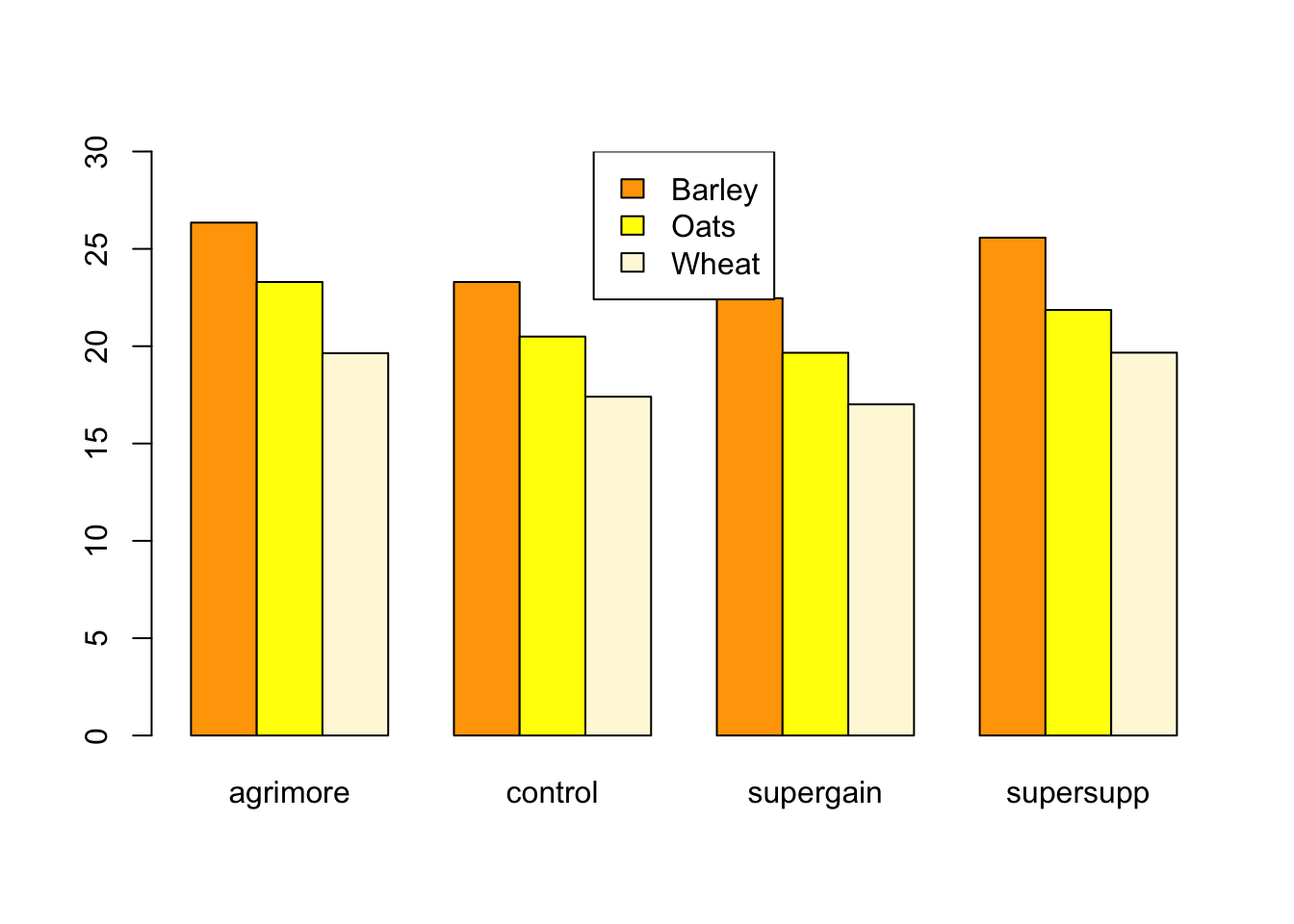
10.7.3 ANOVA
model <- aov(gain ~ diet*supplement, data = weights)
summary(model) Df Sum Sq Mean Sq F value Pr(>F)
diet 2 287.17 143.59 83.52 3.00e-14 ***
supplement 3 91.88 30.63 17.82 2.95e-07 ***
diet:supplement 6 3.41 0.57 0.33 0.917
Residuals 36 61.89 1.72
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Ver interacciones completas
summary.lm(model)
Call:
aov(formula = gain ~ diet * supplement, data = weights)
Residuals:
Min 1Q Median 3Q Max
-2.48756 -1.00368 -0.07452 1.03496 2.68069
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 26.3485 0.6556 40.191 < 2e-16 ***
dietoats -3.0501 0.9271 -3.290 0.002248 **
dietwheat -6.7094 0.9271 -7.237 1.61e-08 ***
supplementcontrol -3.0518 0.9271 -3.292 0.002237 **
supplementsupergain -3.8824 0.9271 -4.187 0.000174 ***
supplementsupersupp -0.7732 0.9271 -0.834 0.409816
dietoats:supplementcontrol 0.2471 1.3112 0.188 0.851571
dietwheat:supplementcontrol 0.8183 1.3112 0.624 0.536512
dietoats:supplementsupergain 0.2470 1.3112 0.188 0.851652
dietwheat:supplementsupergain 1.2557 1.3112 0.958 0.344601
dietoats:supplementsupersupp -0.6650 1.3112 -0.507 0.615135
dietwheat:supplementsupersupp 0.8024 1.3112 0.612 0.544381
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.311 on 36 degrees of freedom
Multiple R-squared: 0.8607, Adjusted R-squared: 0.8182
F-statistic: 20.22 on 11 and 36 DF, p-value: 3.295e-12Modelo muy complejo, por lo que podemos dejar solo los componentes e interacciones significativas e interesantes.
10.7.4 Test de varianzas homogeneas
bartlett.test(gain ~ diet, data = weights)
Bartlett test of homogeneity of variances
data: gain by diet
Bartlett's K-squared = 2.2513, df = 2, p-value = 0.3244bartlett.test(gain ~ supplement, data = weights)
Bartlett test of homogeneity of variances
data: gain by supplement
Bartlett's K-squared = 0.57513, df = 3, p-value = 0.9021model2 <- aov(gain ~ diet + supplement, data = weights)
summary(model2) # ya no hay interacciones! Df Sum Sq Mean Sq F value Pr(>F)
diet 2 287.17 143.59 92.36 4.20e-16 ***
supplement 3 91.88 30.63 19.70 3.98e-08 ***
Residuals 42 65.30 1.55
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1summary.lm(model2)
Call:
aov(formula = gain ~ diet + supplement, data = weights)
Residuals:
Min 1Q Median 3Q Max
-2.30792 -0.85929 -0.07713 0.92052 2.90615
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 26.1230 0.4408 59.258 < 2e-16 ***
dietoats -3.0928 0.4408 -7.016 1.38e-08 ***
dietwheat -5.9903 0.4408 -13.589 < 2e-16 ***
supplementcontrol -2.6967 0.5090 -5.298 4.03e-06 ***
supplementsupergain -3.3815 0.5090 -6.643 4.72e-08 ***
supplementsupersupp -0.7274 0.5090 -1.429 0.16
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.247 on 42 degrees of freedom
Multiple R-squared: 0.8531, Adjusted R-squared: 0.8356
F-statistic: 48.76 on 5 and 42 DF, p-value: < 2.2e-1610.7.5 Comparación de modelos
model: Factorialmodel2: Aditivo
# diferencias significativas entre los dos modelos?
anova(model, model2) # NoAnalysis of Variance Table
Model 1: gain ~ diet * supplement
Model 2: gain ~ diet + supplement
Res.Df RSS Df Sum of Sq F Pr(>F)
1 36 61.890
2 42 65.296 -6 -3.4058 0.3302 0.9166AIC(model, model2) df AIC
model 13 174.4179
model2 7 164.9892# plot(PostHocTest(model, method = "hsd"))
TukeyHSD(model) Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = gain ~ diet * supplement, data = weights)
$diet
diff lwr upr p adj
oats-barley -3.092817 -4.225918 -1.959715 3e-07
wheat-barley -5.990298 -7.123399 -4.857196 0e+00
wheat-oats -2.897481 -4.030582 -1.764379 1e-06
$supplement
diff lwr upr p adj
control-agrimore -2.6967005 -4.138342 -1.2550592 0.0000764
supergain-agrimore -3.3814586 -4.823100 -1.9398173 0.0000015
supersupp-agrimore -0.7273521 -2.168993 0.7142892 0.5326710
supergain-control -0.6847581 -2.126399 0.7568832 0.5817637
supersupp-control 1.9693484 0.527707 3.4109897 0.0040534
supersupp-supergain 2.6541065 1.212465 4.0957478 0.0000972
$`diet:supplement`
diff lwr upr p adj
oats:agrimore-barley:agrimore -3.050093860 -6.2861072 0.1859194 0.0800774
wheat:agrimore-barley:agrimore -6.709404652 -9.9454179 -3.4733914 0.0000010
barley:control-barley:agrimore -3.051827710 -6.2878410 0.1841856 0.0797364
oats:control-barley:agrimore -5.854812782 -9.0908261 -2.6187995 0.0000156
wheat:control-barley:agrimore -8.942959440 -12.1789727 -5.7069461 0.0000000
barley:supergain-barley:agrimore -3.882353990 -7.1183673 -0.6463407 0.0081992
oats:supergain-barley:agrimore -6.685474160 -9.9214875 -3.4494609 0.0000011
wheat:supergain-barley:agrimore -9.336046198 -12.5720595 -6.1000329 0.0000000
barley:supersupp-barley:agrimore -0.773175055 -4.0091883 2.4628382 0.9993538
oats:supersupp-barley:agrimore -4.488243097 -7.7242564 -1.2522298 0.0012832
wheat:supersupp-barley:agrimore -6.680136725 -9.9161500 -3.4441234 0.0000011
wheat:agrimore-oats:agrimore -3.659310793 -6.8953241 -0.4232975 0.0156910
barley:control-oats:agrimore -0.001733850 -3.2377471 3.2342794 1.0000000
oats:control-oats:agrimore -2.804718923 -6.0407322 0.4312944 0.1426161
wheat:control-oats:agrimore -5.892865580 -9.1288789 -2.6568523 0.0000138
barley:supergain-oats:agrimore -0.832260130 -4.0682734 2.4037532 0.9987355
oats:supergain-oats:agrimore -3.635380300 -6.8713936 -0.3993670 0.0167992
wheat:supergain-oats:agrimore -6.285952338 -9.5219656 -3.0499390 0.0000038
barley:supersupp-oats:agrimore 2.276918805 -0.9590945 5.5129321 0.3975577
oats:supersupp-oats:agrimore -1.438149237 -4.6741625 1.7978641 0.9151137
wheat:supersupp-oats:agrimore -3.630042865 -6.8660562 -0.3940296 0.0170562
barley:control-wheat:agrimore 3.657576943 0.4215636 6.8935902 0.0157690
oats:control-wheat:agrimore 0.854591870 -2.3814214 4.0906052 0.9983978
wheat:control-wheat:agrimore -2.233554788 -5.4695681 1.0024585 0.4258079
barley:supergain-wheat:agrimore 2.827050663 -0.4089626 6.0630640 0.1356315
oats:supergain-wheat:agrimore 0.023930493 -3.2120828 3.2599438 1.0000000
wheat:supergain-wheat:agrimore -2.626641545 -5.8626548 0.6093717 0.2089804
barley:supersupp-wheat:agrimore 5.936229597 2.7002163 9.1722429 0.0000120
oats:supersupp-wheat:agrimore 2.221161555 -1.0148517 5.4571748 0.4340350
wheat:supersupp-wheat:agrimore 0.029267927 -3.2067454 3.2652812 1.0000000
oats:control-barley:control -2.802985073 -6.0389984 0.4330282 0.1431702
wheat:control-barley:control -5.891131730 -9.1271450 -2.6551184 0.0000139
barley:supergain-barley:control -0.830526280 -4.0665396 2.4054870 0.9987590
oats:supergain-barley:control -3.633646450 -6.8696597 -0.3976332 0.0168823
wheat:supergain-barley:control -6.284218488 -9.5202318 -3.0482052 0.0000039
barley:supersupp-barley:control 2.278652655 -0.9573606 5.5146659 0.3964466
oats:supersupp-barley:control -1.436415387 -4.6724287 1.7995979 0.9157324
wheat:supersupp-barley:control -3.628309015 -6.8643223 -0.3922957 0.0171405
wheat:control-oats:control -3.088146658 -6.3241600 0.1478666 0.0728783
barley:supergain-oats:control 1.972458793 -1.2635545 5.2084721 0.6078579
oats:supergain-oats:control -0.830661377 -4.0666747 2.4053519 0.9987572
wheat:supergain-oats:control -3.481233415 -6.7172467 -0.2452201 0.0258844
barley:supersupp-oats:control 5.081637727 1.8456244 8.3176510 0.0001928
oats:supersupp-oats:control 1.366569685 -1.8694436 4.6025830 0.9382729
wheat:supersupp-oats:control -0.825323943 -4.0613372 2.4106894 0.9988273
barley:supergain-wheat:control 5.060605450 1.8245922 8.2966187 0.0002063
oats:supergain-wheat:control 2.257485280 -0.9785280 5.4934986 0.4101108
wheat:supergain-wheat:control -0.393086758 -3.6291001 2.8429265 0.9999993
barley:supersupp-wheat:control 8.169784385 4.9337711 11.4057977 0.0000000
oats:supersupp-wheat:control 4.454716343 1.2187030 7.6907296 0.0014257
wheat:supersupp-wheat:control 2.262822715 -0.9731906 5.4988360 0.4066453
oats:supergain-barley:supergain -2.803120170 -6.0391335 0.4328931 0.1431270
wheat:supergain-barley:supergain -5.453692208 -8.6897055 -2.2176789 0.0000577
barley:supersupp-barley:supergain 3.109178935 -0.1268344 6.3451922 0.0691463
oats:supersupp-barley:supergain -0.605889108 -3.8419024 2.6301242 0.9999375
wheat:supersupp-barley:supergain -2.797782735 -6.0337960 0.4382306 0.1448433
wheat:supergain-oats:supergain -2.650572038 -5.8865853 0.5854413 0.1989133
barley:supersupp-oats:supergain 5.912299105 2.6762858 9.1483124 0.0000130
oats:supersupp-oats:supergain 2.197231062 -1.0387822 5.4332444 0.4500973
wheat:supersupp-oats:supergain 0.005337435 -3.2306759 3.2413507 1.0000000
barley:supersupp-wheat:supergain 8.562871143 5.3268578 11.7988844 0.0000000
oats:supersupp-wheat:supergain 4.847803100 1.6117898 8.0838164 0.0004093
wheat:supersupp-wheat:supergain 2.655909473 -0.5801038 5.8919228 0.1967179
oats:supersupp-barley:supersupp -3.715068042 -6.9510813 -0.4790547 0.0133696
wheat:supersupp-barley:supersupp -5.906961670 -9.1429750 -2.6709484 0.0000132
wheat:supersupp-oats:supersupp -2.191893628 -5.4279069 1.0441197 0.4537097# plot(TukeyHSD(model))